Приведенный в статье пример расчетов, связанных с НДС-облигациями, интересен и поучителен. Вы увидите, как «барахтались» авторы, чтобы разобраться в тонкостях данного финансового инструмента. Принцип был ясен сразу, а точный расчет появился довольно поздно (хорошо, что не слишком поздно). Что помешало? Современная «болезнь»: слишком много дел, привычка решать интуитивно и быстро. А когда научный вопрос «пришел в практику», оказалось, что некогда подумать… Знакомо?
Облигационная реструктуризация госдолга
В течение 2009 г. правительство Юлии Тимошенко накопило огромные долги перед украинскими предприятиями. Механизм был прост и скандален: НДС «на выходе» собирался, а «на входе» не возвращался (см. Налоговый кодекс, который в этой части в России и Украине совпадает). Получалась фантастическая схема: НДС брался не с добавленной стоимости, а с выручки, с оборота. Конечно, брали взаймы. В результате накопился многомиллиардный долг правительства перед предприятиями. В 2010 г. президентом Украины был избран Виктор Янукович, а на смену правительству Юлии Тимошенко пришло правительство Николая Азарова. Новое правительство столкнулось с проблемой: с одной стороны, невозвращенный НДС — долг, а отдавать долги — дело чести и разума. С другой — отдать все и сразу невозможно. Выход был найден: возмещать долги путем выпуска облигаций, которые в народе назвали НДС-облигациями.
Это пример идеального решения проблемы: и волки сыты, и овцы целы. Кроме того, была найдена удачная схема погашения долга. Новое украинское правительство обязательства по НДС-облигациям пока полностью выполняет.
Обратите внимание
На рынок НДС-облигаций пришла масса новых игроков — предприятий, до сей поры незнакомых с фондовым рынком. Здесь ярко проявился эффект асимметрии информации: одни участники «знают» (банки и другие финансовые институты), остальные (предприятия) — «не знают». В результате одни выигрывают, другие остаются не у дел, мол, на предприятиях давно появились финансовые директора, пусть они и решают. Вот только умеют ли?
Параметры НДС-облигаций
НДС-облигации — это государственные облигации с фиксированной купонной ставкой и амортизацией тела (табл. 1). Правительство Украины решило эмитировать их в счет долга по возмещению НДС. Количество облигаций определяется суммой долга.
Особенности НДС-облигаций:
1) облигация была амортизируемой, то есть гасилась каждые полгода равными частями. Это объясняется тем, что предприятия должны пополнить оборотные средства как можно раньше. Поэтому амортизация — удачный компромисс между острой нуждой предприятий и полупустой государственной казной;
2) условность первого числа денежного потока. Обычно держатель облигации вначале покупает ее, то есть тратит деньги. С НДС-облигациями все иначе.
Перейдем к примеру. Итак, 9 сентября 2010 г. предприятие Х получило на счет большое количество НДС-облигаций, а «платило» милостью правительства Тимошенко гораздо раньше и частями. Поэтому только условно денежный поток 9 сентября можно считать равным –1000 грн. (табл. 2).
Поиск постановки задачи и ее первоначальное решение
На счет предприятия Х 9 сентября 2010 г. была зачислена крупная сумма в виде облигаций. Финансовые руководители задумались: что с ними делать? В результате возникла альтернатива:
- продать облигации и получить деньги, которые можно реинвестировать в производство или покрыть долги;
- держать хотя бы часть облигаций. С чем сравнивать? Например, можно продать некоторое количество и вырученные деньги вложить в другой финансовый инструмент с большей доходностью (допустим, положить на депозит. В сентябре 2010 г. это можно было сделать под 15% годовых против 5,5% по НДС‑облигациям). Более того, НДС-облигации более ликвидны, чем срочный вклад.
Выбрали два базовых варианта:
- держать облигации до конца срока обращения (до 29 октября 2015 г.);
- продать с дисконтом, а вырученные деньги положить на депозит на тот же срок.
Вначале, интуитивно оценив доходность облигаций как низкую, решили их реализовать. Тем более что от разных финансовых учреждений начали поступать предложения продать облигации с дисконтом, размер которого колебался от 21 до 18%. Систематизация поступивших предложений была поручена финансисту Василию.
Приступая к работе, Василий решил освежить знания по финансовой математике. И начались сомнения: избавляться от облигаций или нет?
10 ноября 2010 г. на предприятие Х приехал преподаватель из Москвы Андрей Мицкевич. Василий обратился к нему за помощью в вопросе финансовой математики: как разобраться с облигациями, тем более что сумма весьма значительная?
— Василий, вы, конечно, помните APR, IRR, NPV и подобные показатели? — спросил Андрей Алексеевич.
— При выполнении дипломной работы по оценке бизнеса я хорошо усвоил понятия NPV и IRR. А вот APR не припоминаю.
— По сути, IRR и APR — одно и то же, — Андрей Алексеевич изобразил графики потоков, расчеты показателей, а заодно и определение понятий APR и IRR. Оказалось, на языке математики это идентичные вещи:
APR = IRR : NPV (IRR) = 0.
— Ясно, что IRR — это такая ставка дисконтирования, которая обнуляет NPV.
— Кстати, — поинтересовался Андрей Алексеевич, — в бизнес-школе вас учили пользоваться финансовыми функциями Excel?
— Нет!
— Как обычно, на практику времени не хватило. Его действительно мало, а мы гонимся за высокой теорией. Рейтинги и прочие «московские штучки» мешают объяснить самое важное: как считать…
К утру 11 ноября 2010 г. анализ обрел форму. Василий для начала расписал денежные потоки от одной облигации (табл. 3).
В обеденный перерыв наши герои опять встретились. Василий показал Андрею таблицу 3.
— На первый взгляд правильно. Как это у тебя получилось?
— Вот она, облигация, во всей красе денежных потоков, но что с ней делать дальше, с чем сравнивать, какие критерии просчитать? Нужна какая-то система!
— Нет проблем, — сказал Андрей, — просчитай выгоды банка и предприятия при разных дисконтах. Дисконт — это минимальные 18%, которые банк предлагал тебе 9 сентября. Сравни варианты «Держать» и «Продать».
— Какие критерии использовать?
— «Задержать обычных подозреваемых…»: NPV и IRR. Да и так все почти понятно… — сказал Андрей.
Василий размышлял, зачем считать выгоды банка. Пусть банк сам разбирается...
Поскольку Василий сидел за компьютером и быстро освоил урок про финансовые функции в Excel, то решил оперативно просчитать самый главный показатель — NPV. Он взял «среднепотолочную» украинскую ставку требуемой доходности 25% и, поделив пополам, получил 12,5% — ставку дисконтирования за полгода.
Обратите внимание
NPV — это чистый дисконтированный (приведенный) доход (стоимость) — самый важный показатель (критерий выбора) инвестиционного проекта. Данный термин лучше не переводить на русский язык — это только создаст путаницу. И в Китае, и в Греции, и в России вас поймут, если вы скажете NPV или Net Present Value.
Расчет NPV требует задать ставку дисконтирования. Какую выбрать?
В Украине инфляция выше, чем в России. Других рисков по крайней мере не меньше. Для ускоренной отработки методики решения задачи годовую ставку дисконтирования приняли равной 25%.
Какую ставку взять, чтобы она пригодилась и для равновесных расчетов (для поиска равновыгодного дисконта для банка и предприятия, когда они получают одинаковый PV — знаменитое «деление поровну»)? На вопрос, почему PV, а не NPV, ответим позже.
В принципе банк должен дисконтировать по своей ставке, а предприятия — по своей. Но мы «не видим» ставки дисконтирования банка в момент переговоров. Как быть?
Решение: пока возьмем 25% и будем думать над другими вопросами. Первый расчет NPV, вариант «Держать». Василий сделал грубую прикидку. Он понимал, что NPV1 (10 раз по полгода) означает весьма приближенный расчет: брали старт с 29 октября 2010 г. вместо точной даты — 9 сентября 2010 г. (результат — в табл. 4).
Второй расчет NPV, вариант «Держать». Вечером Василий вспомнил, чему его учили на курсе «Инвестиционный проект». Должна быть точная ставка дисконтирования, рассчитанная так, чтобы эффективная ставка процента составляла 25% за год, то есть (1 + + RD1/2)2 = 1,25, где RD1/2 — полугодовая ставка дисконтирования. Получилась точная ставка ![]() или 11,8%.
или 11,8%.
Обратите внимание
Поясним, как считать точную ставку дисконтирования. Итак, 25% за год. Деньги растут по сложному проценту. Обозначим х темп прироста в долях за полгода. Тогда за первые полгода темп роста финансового инструмента составит (1 + х ). В нашем случае таким инструментом можно считать полугодовой коэффициент дисконтирования (1 + RD). За год темп роста получится (1 + х)2, он должен совпасть с коэффициентом дисконтирования за год, то есть: (1 + RD)2 = 1,25.
Многие практически значимые решения оформляются в виде инвестиционного проекта с месячным шагом. Для их правильного подсчета следует вычислить месячную ставку дисконтирования. Ее легко можно рассчитать аналогично: (1 + RD1/12)12 = 1,25. Получаем RD1/12 = 1,88.
Василий вспомнил еще один показатель: IRR = APR. По‑прежнему он считал с 29 октября 2010 г. по 29 октября 2015 г. (табл. 5).
Расчет проводился по формуле:
![]() .
.
Примечание: данные CIF взяты из табл. 3.
Расчет NPV и IRR, вариант «Продать». Сначала Василий рассчитал денежные потоки (табл. 6). Обратите внимание на первый элемент денежного потока — предположение, что мы жертвуем номиналом облигации –1000 грн.
Допущения:
1) выплаты процента банком привязаны к календарному месяцу и выплачиваются в последний день. Это предположение есть еще один резерв для уточнения расчетов. Но уж очень мала ошибка, потому Василий ею сначала пренебрег;
2) первый элемент денежного потока — предположение, что мы жертвуем номиналом облигации –1000 грн. (Так ли это на самом деле?);
3) использовалась точная ставка процента.
Для расчета точного процента с точным числом дней в России, как правило, применяется формула:
![]()
Она обязательна для российских банков в соответствии с Положением ЦБ РФ от 26.06.98. Используют точный процент с базой в 365 или 366 дней (указывается точное число). Формула применяется и для кредитов, и для депозитов. Процент начисляется ежедневно в 9.00 в момент открытия банка до дня фактического закрытия счета включительно.
Василий по-прежнему грубо обошелся со временем: считал с 29 октября 2010 г. по 29 октября 2015 г. вместо точной даты старта 9 сентября 2010 г. В результате получилась табл. 7.
Точная ставка дисконтирования периода (месяц) вычислялась по формуле:
![]() .
.
NPV отрицателен: что делать? Это означает, что требуемую доходность в 25% любой вариант не обеспечивает. Выходит, от данных вариантов следует отказываться? Нет. Просто выбираем из двух зол меньшее.
12 ноября в задаче появилось новое понятие: равновесная ставка дисконта банка. Что это?
Торгуясь, люди (чаще всего из уважения) стремятся «делить поровну». Но хорошо известно, что в деталях деления поровну скрыт дьявол. Экономист сразу вспомнит: как делить прибыль — по ее сумме (массе) или по равной норме? Юрист приведет пример невозможности точного деления пополам имущества при разводе супругов.
Андрей посоветовал подсчитать такой дисконт, который уравняет выгоду от вариантов «Держать» и «Продать».
Василий посчитал его просто: подставляя значения и постепенно уравнивая результат в Excel. Но так как формул было две, то и результатов оказалось два (по NPV и по IRR):
— по NPV получилось 8,93%:
NPV (дата 9 сентября 2010 г., решение «держать», RD = 25%) = = –295,27 грн. = NPV (дата 9 сентября 2010 г., решение «продать», равновесный дисконт банка
RD = 25%, I — ставка и другие условия депозита).
Читать формулу надо так:
- анализ и вычисления равновесного дисконта проводятся на определенную дату: (в данном расчете на 9 сентября 2010 г.);
- NPV решения «держать» на 9 сентября 2010 г. известно: –295,27 грн. (табл. 5);
- найдем такой дисконт банка, который дает от решения «продать» тот же NPV;
— по IRR получилось 30,73%.
IRR (дата, решение «держать») = 5,28% = IRR (дата, решение «продать», равновесный дисконт банка, I — ставка и другие условия депозита).
Начнем с более понятной цифры: 8,93%. Что она означает? Банк дает 18% дисконта. Получается, «держать» намного выгоднее. Но равновесный IRR — 30,73%! Как этот результат интерпретировать?
Кстати, когда Василий поинтересовался, зачем нужны эти расчеты, то получил ответ: банкиры испугаются, что он так хорошо считает. Действительно, в январе 2011 г. Василию удалось значительно снизить ставку дисконтирования. Банкиры скинули по сравнению с рынком 3—5%. Так теория дала первый практический результат, хотя и была с ошибками…
Подведем итоги: на основе финансовой математики в такой постановке задачи принято решение «держать». Оно пока совпадает с интуитивным решением Василия.
Правильная постановка задачи и ее решение в общем случае
По окончании занятий Андрей Алексеевич вернулся в Москву. Они с Василием продолжили общение через Интернет. К проекту подключили Анастасию, студентку магистратуры НИУ ВШЭ.
Ближе к лету Андрей и Анастасия, разрабатывая методику решения данной задачи, обнаружили две ошибки — принципиальную и счетную. Начнем со второй.
Счетная ошибка: приближенные даты. Все расчеты велись от 29 октября 2010 г. до 29 октября 2015 г. А надо считать точно: от 9 сентября 2010 г. до 29 октября 2015 г. Выход прост — в формуле
![]()
следует ввести поправку на время. Интервал в 50 дней при ставке дисконтирования 25% дает существенную ошибку. К счастью, ее легко демпфировать.
Обозначим за PV (29 октября) = ![]() .
.
Это PV надо привести к 9 сентября. Разница в 50 дней при украинской ставке дисконтирования существенна:
PV (9 сентября) = PV (29 октября) х 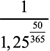 .
.
В результате точная формула будет такой:
![]() .
.
Итог пересчета — в табл. 8.
–316,47 против –363,64 — очень существенная ошибка. Дальнейшие вычисления приведены в «точном» формате.
Принципиальная ошибка: включение «утопленных» затрат. Мы считали, что 9 сентября 2010 г. денежный поток равен –1000 грн. (теряем облигацию, потому и минус 1000). Но условность первого числа денежного потока очевидна: мы никому ничего не платим, а только получаем. Когда образовался долг — несколько лет назад, — никакого отношения не имеет к платежам по НДС-облигациям, и это не должно влиять на расчеты.
Вывод 1. Денежный поток (CIF) 9 сентября равен 0, а не –1000. Затраты «утоплены», как говорят специалисты по инвестиционным проектам. Безошибочные денежные потоки приведены в табл. 9.
Вывод 2. Расчеты по IRR = = APR и по NPV прекратить и перейти к PV. Расчет вести на дату 9 сентября 2010 г.
Результаты пересчета все ставят на свои места: получение облигаций — благо, NPV = NPV, NPV больше 0. Нет больше противоречий и странных результатов (табл. 10).
Примечание. NPV рассчитаны на 9 сентября 2010 г. по формуле:
- PV (ДЕРЖАТЬ, 9 сентября) = PV (ДЕРЖАТЬ, 30 апреля 2011 г.) х
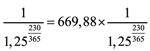 ;
;
- PV (ПРОДАТЬ, 9 сентября) = PV (ПРОДАТЬ, 30 сентября 2010 г.) х
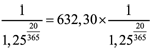 .
.
Вывод очевиден: «продать» намного выгоднее. Интуитивное решение Василия было НЕВЕРНЫМ! Теперь надо срочно выдать общее решение и вооружить Василия правильным инструментарием.
Правильная постановка задачи
Наконец-то стала прозрачной постановка задачи. Система денежных потоков для сравниваемых базовых решений на дату Т:
1) «продать» облигации с дисконтом Д и в тот же день вложить полученные деньги в банк на депозит под процент I с месячной капитализацией (считаем, что выплаты приходятся на конец месяца);
2) «держать» облигации до срока погашения.
Все денежные потоки до даты Т нерелевантны: они одинаковы для обоих базовых решений и поэтому не учитываются, включая выплаты купонных процентов. Поэтому условность первого числа денежного потока (вторая особенность НДС‑облигаций, см. выше) несущественна для нашей задачи. Принимаем всегда CIF (T) = 0.
Правило формирования CIF:
- выплаты процента банком привязаны к календарному месяцу и выплачиваются в его последний день;
- первый элемент денежного потока всегда равен 0.
Критерий принятия решений: в современной постановке финансового менеджмента он выглядит так: какой денежный приток (от решения «держать» или «продать») больше увеличивает ценность предприятия? В результате надо сравнить два числа:
- PV (дата, решение «держать», RD = 25%);
- PV (дата, решение «продать», дисконт банка, RD = 25%, I — ставка процента по депозитам, другие условия депозита).
Затем следует выбрать большее значение NPV. Этот вариант выгоднее предприятию при отсутствии «денежного голода».
Ставка дисконтирования RD = = 25% выбрана как среднеукраинская для отрасли предприятия Х в соответствии с моделью САРМ. На реальных торгах ставку надо пересчитывать и вводить все реальные условия.
Равновесный дисконт для торга с банком: целесообразно снабдить ЛПР равновесной ставкой дисконта банка, вычисляемой из уравнения:
PV (дата, решение «держать», RD) = PV (дата, решение «продать», равновесный дисконт банка, RD, I, другие условия депозита).
Равновесная ставка дисконта банка обеспечивает равную выгодность обоих вариантов для предприятия, поэтому на переговорах можно просто сравнивать предлагаемый дисконт с равновесным:
- если предлагаемый дисконт меньше равновесного, выгоднее «продать»;
- если предлагаемый дисконт больше равновесного, выгоднее «держать».
Бесплатных ошибок не бывает
Как выяснилось, неправильная постановка задачи приводит к ошибкам. Их игнорирование влечет серьезные погрешности при расчете равновесного дисконта. В итоге торги с банком могут пройти не в нашу пользу.
Величина ошибок может превысить 10 млн грн. (более 2 млн руб.: равновесный дисконт, рассчитанный по критерию IRR, составляет около 30% против точной оценки 23,59%), что дает ошибку в большую сторону. Это может привести к принятию заведомо невыгодных для предприятия условий банка. Напомним, что при правильной постановке задачи этот критерий неприменим, поскольку нет отрицательного денежного оттока. Кстати, это именно тот главный случай, когда критерий IRR не работает.
Рассмотрим, насколько серьезными могут оказаться последствия ошибок при расчете равновесного дисконта по критерию NPV. Ниже представлены величины равновесного дисконта при различных вариантах расчета PV и NPV при условии, если сделка состоится 9 сентября 2010 г. (табл. 11).
Как видим, погрешность высока — равновесный дисконт для NPV (грубо: 10 раз по полгода, точная ставка дисконтирования) отличается от соответствующего PV: 23,59% – 8,93% = 14,66%.
Особенно сильно неучтенная принципиальная ошибка — включение «утопленных» затрат — портит равновесный дисконт: 23,59% – 11,74% = 11,85%.
Рассчитывая равновесный дисконт по методу Василия, мы ошиблись в меньшую сторону, то есть при переговорах будем требовать заниженный дисконт. Банк может не согласиться, и сделка не состоится даже при выгодных для обеих сторон условиях.
Анализ вариантов решений
Применим полученный инструментарий к двум датам: до первой купонной выплаты и после.
Вариант 1
21 января 2011 г. Василий проанализировал только базовые решения, выбирая между ними:
продать облигации с дисконтом 9,92% и в тот же день — 21 января — положить полученные деньги на депозит под 15% годовых с месячной капитализацией или выплатой процента. В условиях высокой ставки дисконтирования выгоднее получать проценты, а не прибавлять их к сумме депозита. Обратите внимание на размер дисконта по сравнению с сентябрем — ноябрем. Такой неплохой дисконт был предложен банкиром, который увидел, что Василий «умеет считать»;
держать облигации до срока погашения (29 октября 2015 г.).
Таблицы денежных потоков читателю нужно сформировать самому. Обратите внимание на изменения: 9,92% — результат работы рынка и Василия, которому теперь предлагают лучшие условия, нежели рыночные. Как думаете почему? Результаты расчетов — в табл. 12.
PV рассчитаны на 21 января 2011 г. по формулам:
30 апреля 2011 г. – 21 января 2011 г. = 99.
- PV (ДЕРЖАТЬ, 21 января 2011 г.) = PV (ДЕРЖАТЬ, 30 апреля 2011 г.) х
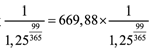 ;
;
- PV (ПРОДАТЬ, 21 января 2011 г.) = PV (ПРОДАТЬ, 30 сентября 2010 г.) х
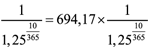 ;
;
- равновесный дисконт составляет 17,677%.
Вывод тот же, что и вначале — 9 сентября 2010 г.: «продать» намного выгоднее.
Новое интуитивное решение Василия (по-прежнему «держать») было неверным.
Вариант 2
1 июня 2011 г. Андрей и Анастасия, выявив все неточности, решили пересчитать результаты на текущую дату. Таблицы 13 и 14 содержат денежные потоки двух вариантов.
29 октября 2011 г. – 1 июня 2011 г. = 151.
- PV (ДЕРЖАТЬ, 1 июня 2011 г.) = PV (ДЕРЖАТЬ, 29 октября 2011 г.) х
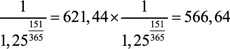 .
.
30 июня 2011 г. – 1 июня 2011 г. = 30.
- PV (ПРОДАТЬ, 1 июня 2011 г.) = PV (ПРОДАТЬ, 30 июня 2011 г.) х
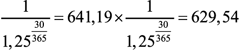 ;
;
- равновесный дисконт = 18,92%.
Вывод тот же: «продать» намного выгоднее. Срочно звоним Василию…
В таблице 16 для справки приведено описание финансовых функций в Excel, применяемых для расчета вышеуказанных показателей.
Параметры НДС-облигации (таблица 1)
|
Параметр |
Значение |
|
Номинал |
1000 грн. (около 3900 руб.) |
|
Срок обращения |
5 лет |
|
Количество выплат в год |
2 раза |
|
Купонная ставка* |
5,5% годовых |
|
Дата выпуска (для рассматриваемого примера) |
09.09.10 |
|
Амортизация периода — 10% номинала** |
100 грн. |
* Купонный процент начисляется на остаток долга (актуарная схема).
**Амортизация тела: номинал (1000 грн.) делится на 10 частей и по одной части (100 грн.) выплачивается раз в полгода в придачу к купону.
Денежные потоки от одной облигации, вариант «Держать» (расчет на 11 ноября 2010 г.) (таблица 2)
|
09.09.10 |
30.04.11 |
29.10.11 |
30.04.12 |
29.10.12 |
30.04.13 |
29.10.13 |
30.04.14 |
29.10.14 |
30.04.15 |
29.10.15 |
|
–1000 |
127,5 |
124,75 |
122 |
119,25 |
116,5 |
113,75 |
111 |
108,25 |
105,5 |
102,75 |
Расчет денежных потоков от одной облигации, вариант «Держать», грн. (таблица 3)
|
Сроки выплат |
Амортизация тела облигации |
Купонный платеж |
Платежи |
|
9 сентября 2010 г. |
–1000 | ||
|
30 апреля 2011 г. |
1000,00 |
27,50 (1000 х 0,055 : 2) |
127,50 |
|
29 октября 2011 г. |
900,00 (1000–1000 х 0,1) |
24,75 (900 х 0,055 : 2) |
124,75 |
|
30 апреля 2012 г. |
800,00 |
22,00 |
122,00 |
|
29 октября 2012 г. |
700,00 |
19,25 |
119,25 |
|
30 апреля 2013 г. |
600,00 |
16,50 |
116,50 |
|
29 октября 2013 г. |
500,00 |
13,75 |
113,75 |
|
30 апреля 2014 г. |
400,00 |
11,00 |
111,00 |
|
29 октября 2014 г. |
300,00 |
8,25 |
108,25 |
|
30 апреля 2015 г. |
200,00 |
5,50 |
105,50 |
|
29 октября 2015 г. |
100,00 |
2,75 |
102,75 |
Первый расчет NPV, вариант «Держать» (11 ноября 2010 г., день) (таблица 4)
|
Грубая ставка дисконтирования периода (полугодовая по простому проценту) |
12,50% |
|
Грубая прикидка сроков |
Ровно пять лет без учета периода
|
|
NPV |
–309,47 грн. |
Второй расчет NPV, вариант «Держать» (11 ноября 2010 г., вечер) (таблица 5)
|
Точная ставка дисконтирования периода (полугодие) |
11,80% |
|
Грубая прикидка сроков |
Ровно пять лет без учета периода
|
|
NPV2 (грубо: 10 раз по полгода, точная ставка дисконтирования) |
–295,27 грн. |
|
IRR годовая ставка внутренней доходности (использовалась функция Excel ЧИСТВНДОХ) и считалась грубо
|
5,28%
|
Денежные потоки от одной облигации, вариант «Продать» (11 ноября 2010 г., использовалась точная ставка процента), грн. (таблица 6)
|
09.09.10 |
Первый элемент денежного потока — предположение, что мы жертвуем номиналом облигации –1000 грн. | ||||||||||
|
-1000 | |||||||||||
|
30.09.10 |
31.10.10 |
30.11.10 |
31.12.10 |
31.01.11 |
28.02.11 |
31.03.11 |
30.04.11 |
31.05.11 |
30.06.11 |
31.07.11 |
31.08.11 |
|
7,08 |
10,45 |
10,11 |
10,45 |
10,45 |
9,44 |
10,45 |
10,11 |
10,45 |
10,11 |
10,45 |
10,45 |
|
30.09.11 |
31.10.11 |
30.11.11 |
31.12.11 |
31.01.12 |
29.02.12 |
31.03.12 |
30.04.12 |
31.05.12 |
30.06.12 |
31.07.12 |
31.08.12 |
|
10,11 |
10,45 |
10,11 |
10,45 |
10,45 |
9,75 |
10,45 |
10,11 |
10,45 |
10,11 |
10,45 |
10,45 |
|
30.09.12 |
31.10.12 |
30.11.12 |
31.12.12 |
31.01.13 |
28.02.13 |
31.03.13 |
30.04.13 |
31.05.13 |
30.06.13 |
31.07.13 |
31.08.13 |
|
10,11 |
10,45 |
10,11 |
10,45 |
10,45 |
9,44 |
10,45 |
10,11 |
10,45 |
10,11 |
10,45 |
10,45 |
|
30.09.13 |
31.10.13 |
30.11.13 |
31.12.13 |
31.01.14 |
28.02.14 |
31.03.14 |
30.04.14 |
31.05.14 |
30.06.14 |
31.07.14 |
31.08.14 |
|
10,11 |
10,45 |
10,11 |
10,45 |
10,45 |
9,44 |
10,45 |
10,11 |
10,45 |
10,11 |
10,45 |
10,45 |
|
30.09.14 |
31.10.14 |
30.11.14 |
31.12.14 |
31.01.15 |
28.02.15 |
31.03.15 |
30.04.15 |
31.05.15 |
30.06.15 |
31.07.15 |
31.08.15 |
|
10,11 |
10,45 |
10,11 |
10,45 |
10,45 |
9,44 |
10,45 |
10,11 |
10,45 |
10,11 |
10,45 |
10,45 |
|
30.09.15 |
31.10.15 |
Последний платеж включает сумму процента за октябрь 2015 г. плюс выплаты тела депозита 10,45 + 820 = 830,45 | |||||||||
|
10,11 |
830,45 | ||||||||||
Второй расчет NPV, вариант «Продать» (11 ноября 2010 г., вечер. Исходные данные приведены в табл. 2 и 6) (таблица 7)
|
Дисконт банка |
18% |
|
Точная ставка дисконтирования периода (месяц) |
1,88% |
|
NPV2 (грубо: 10 раз по полгода, точная ставка дисконтирования) |
–363,64 грн. |
|
IRR — годовая ставка внутренней доходности (использовалась функция Excel ЧИСТВНДОХ) и считалась грубо с 29 октября 2010 г. по 29 октября 2015 г. |
10,00% |
Третий расчет NPV, вариант «Держать» (Москва, апрель 2011 г.) (таблица 8)
|
NPV3 (точно от 9 сентября 2010 г. до 29 октября 2015 г., точная ставка дисконтирования) |
–316,47 грн.
|
Денежные потоки от одной облигации, вариант «Держать» (расчет в мае 2011 г.) (таблица 9)
|
09.09.10 |
30.04.11 |
29.10.11 |
30.04.12 |
29.10.12 |
30.04.13 |
29.10.13 |
30.04.14 |
29.10.14 |
30.04.15 |
29.10.15 |
|
0 |
127,5 |
124,75 |
122 |
119,25 |
116,5 |
113,75 |
111 |
108,25 |
105,5 |
102,75 |
Точный расчет PV на 9 сентября 2010 г. для двух вариантов при дисконте 18% (исходные данные см. в табл. 6 и 9 (с заменой первого CIF на 0)) (таблица 10)
|
Дисконт банка |
18% |
|
PV («Держать»), точная ставка дисконтирования за полгода = 11,8% |
582,01 грн. |
|
PV («Продать»), точная ставка дисконтирования за месяц = 1,88% |
624,62 грн. |
Сравнение величин равновесного дисконта, рассчитанного на 9 сентября 2010 г. по критерию NPV при полугодовой ставке дисконтирования 11,8% (таблица 11)
|
Принципиальная ошибка | |||
|
есть |
нет | ||
|
Счетная ошибка |
есть |
8,93% |
12,06% |
|
нет |
11,74% |
23,59% | |
Точный расчет PV для двух вариантов при дисконте 9,92% (на 21 января 2011 г.) (таблица 12)
|
Дисконт банка |
9,92% |
|
PV («Держать»), точная ставка дисконтирования за полгода = 11,8% |
630,53 грн. |
|
PV («Продать»), точная ставка дисконтирования за месяц = 1,88% |
689,94 грн. |
Денежные потоки от одной облигации, вариант «Держать» (расчет на 1 июня 2011 г.) (таблица 13)
|
01.06.11 |
29.10.11 |
30.04.12 |
29.10.12 |
30.04.13 |
29.10.13 |
30.04.14 |
29.10.14 |
30.04.15 |
29.10.15 |
|
0 |
124,75 |
122 |
119,25 |
116,5 |
113,75 |
111 |
108,25 |
105,5 |
102,75 |
Денежные потоки от одной облигации, вариант «Продать» (расчет на 1 июня 2011 г.) (таблица 14)
|
30.09.10 |
31.10.10 |
30.11.10 |
31.12.10 |
31.01.11 |
28.02.11 |
31.03.11 |
30.04.11 |
31.05.11 |
30.06.11 |
31.07.11 |
31.08.11 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
10,00 |
10,33 |
10,33 |
|
30.09.11 |
31.10.11 |
30.11.11 |
31.12.11 |
31.01.12 |
29.02.12 |
31.03.12 |
30.04.12 |
31.05.12 |
30.06.12 |
31.07.12 |
31.08.12 |
|
10,00 |
10,33 |
10,00 |
10,33 |
10,33 |
9,64 |
10,33 |
10,00 |
10,33 |
10,00 |
10,33 |
10,33 |
|
30.09.12 |
31.10.12 |
30.11.12 |
31.12.12 |
31.01.13 |
28.02.13 |
31.03.13 |
30.04.13 |
31.05.13 |
30.06.13 |
31.07.13 |
31.08.13 |
|
10,00 |
10,33 |
10,00 |
10,33 |
10,33 |
9,33 |
10,33 |
10,00 |
10,33 |
10,00 |
10,33 |
10,33 |
|
30.09.13 |
31.10.13 |
30.11.13 |
31.12.13 |
31.01.14 |
28.02.14 |
31.03.14 |
30.04.14 |
31.05.14 |
30.06.14 |
31.07.14 |
31.08.14 |
|
10,00 |
10,33 |
10,00 |
10,33 |
10,33 |
9,33 |
10,33 |
10,00 |
10,33 |
10,00 |
10,33 |
10,33 |
|
30.09.14 |
31.10.14 |
30.11.14 |
31.12.14 |
31.01.15 |
28.02.15 |
31.03.15 |
30.04.15 |
31.05.15 |
30.06.15 |
31.07.15 |
31.08.15 |
|
10,00 |
10,33 |
10,00 |
10,33 |
10,33 |
9,33 |
10,33 |
10,00 |
10,33 |
10,00 |
10,33 |
10,33 |
|
30.09.15 |
31.10.15 |
Последний платеж включает сумму процента за октябрь 2015 г. плюс выплаты тела депозита 10,33 + 900 х (1 – 0,0992) = 10,33 + 810,72 = 821,05 | |||||||||
|
10,00 |
821,05 | ||||||||||
Точный расчет PV для двух вариантов при дисконте 9,92% (на 1 июня 2011 г.) (таблица 15)
|
PV («Держать»), точная ставка дисконтирования за полгода = 11,8% |
566,64 грн. |
|
PV («Продать»), точная ставка дисконтирования за месяц = 1,88% |
629,54 грн. |
Финансовые функции в Excel, применяемые для расчета показателей эффективности (таблица 16)
|
Показатель |
Финансовая функция в Excel |
Описание финансовой функции |
|
Эффективная ставка (IRR),
|
ЧИСТВНДОХ (значения денежного потока, даты) |
Рассчитывает доходность «инвестиционного проекта», если операции
|
|
Чистый дисконтированный доход (NPV) |
ЧПС (ставка дисконтирования, |
Рассчитывает текущую стоимость ряда различных по сумме будущих |
|
денежный поток (список значений)) |
платежей, если они осуществляются в конце условных периодов |
